The Philosophy of Fair Machine Learning

This post is devoted to explaining the philosophical underpinnings of both statistics-based and causal fair machine learning metrics.

Statistical

Many of the statistics-based fair machine learning metrics in the fair machine learning literature correspond to the notions of distributive justice from social science literature [1]. Here, I introduce the philosophical ideal of equality of opportunity (EOP) and its three main frames: formal EOP, substantive EOP, and luck-egalitarian EOP.

In [2], Khan et al. propose grounding current (and future) proposed fair machine learning metrics in the moral framework of equality of opportunity (EOP) [3]. EOP is a political ideal that is opposed to assigned-at-birth (caste) hierarchy, but not to hierarchy itself. In a caste hierarchy, a child normally acquires the social status of their parents. Social mobility may be possible, but the process to rise through the hierarchy is open to only specific individuals depending on their initial social status. In contrast to a caste hierarchy, EOP demands that the social hierarchy is determined by a form of equal competition among all members of the society. From a philosophical perspective, EOP is a principle that dictates how desirable positions, or opportunities, should be distributed among members of a society. As a moral framework, EOP allows machine learning practitioners to see fairness notions’ motivations, strengths, and shortcomings in an organized and comparative fashion. Additionally, it presents moral questions that machine learning practitioners must answer to construct a fairness system that satisfies their desired values [2]. Further, it allows practitioners to understand and appreciate why there may be disagreement when it comes to choosing a specific fair machine learning metric, as different people will have different moral beliefs about what fairness and equality mean. The different conceptions of EOP (formal, substantive, and luck-egalitarian EOP) all interpret the idea of competing on equal terms in different ways.

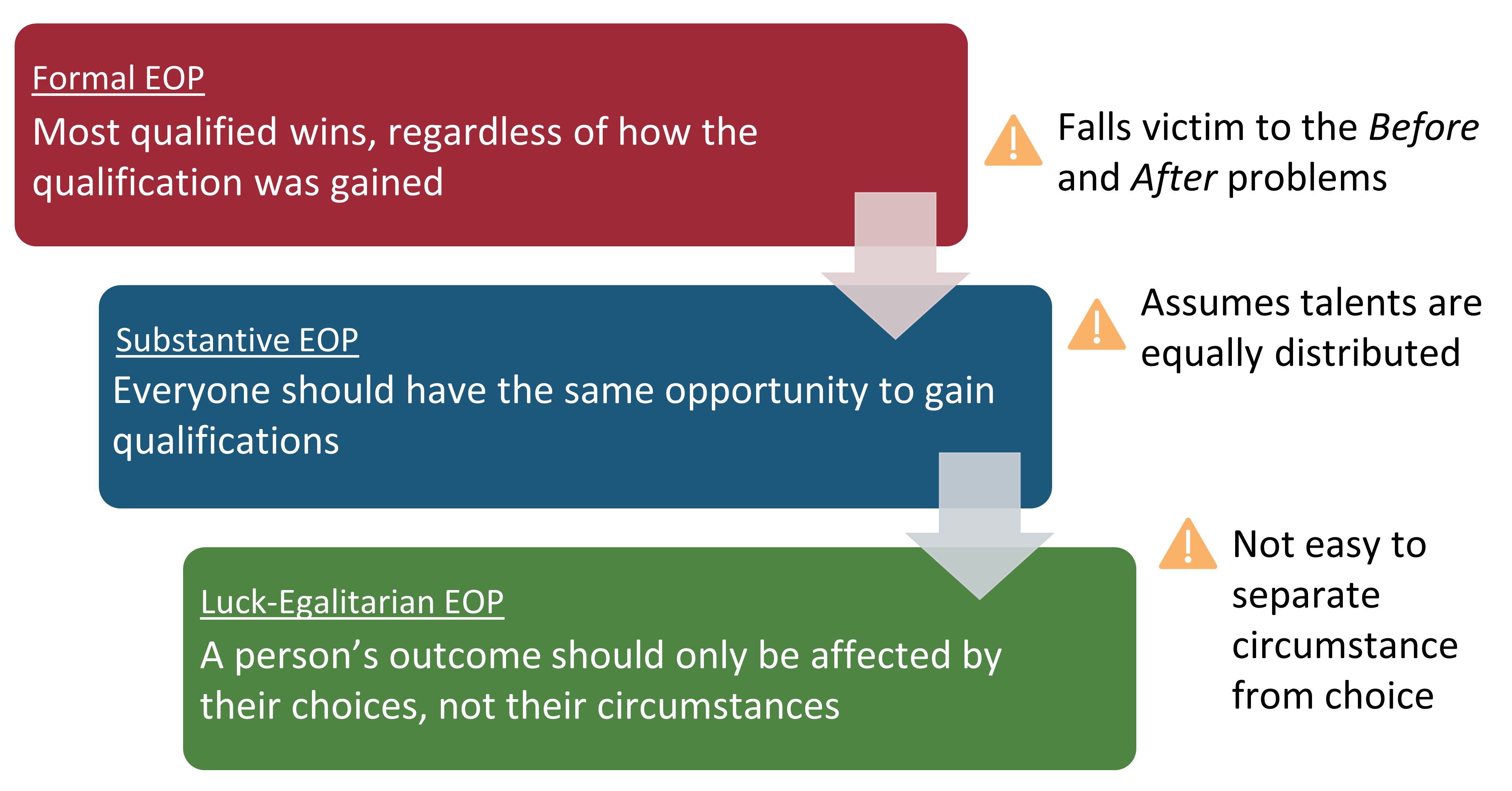
Formal EOP

Formal EOP emphasizes that any desirable position (in a society, or more concretely, a job opening) is available and open to everyone. The distribution of these desirable positions follows according to the individual’s relevant qualifications, and in this setting, the most qualified always wins. Formal EOP takes a step in the direction of making decisions based on relevant criteria rather than making them in a blatant discriminatory fashion [2]. In the fair machine learning setting, formal EOP has often been implemented as fairness through blindness or fairness through unawareness [4]. In other words, formal EOP-based metrics strip away any irrelevant marginalization attributes, such as race or gender, before training is performed.

However, while formal EOP has the benefit of awarding positions based on actual qualifications of an individual, and in excluding irrelevant marginalization information, it makes no attempt to correct for arbitrary privileges. This includes unequal access to opportunities that can lead to disparities between individuals’ qualifications. Examples of this situation can be seen in the task of predicting prospective student’s academic performance for use in college admission decisions [5]. Individuals belonging to marginalized or non-conforming groups, such as Black and/or LGBTQIA+ students, and/or students with disabilities, are disproportionately impacted by the challenges of poverty, racism, bullying, and discrimination. An accurate predictor for a student’s success therefore may not correspond to a fair decision-making procedure as the impact of these challenges create a tax on the “cognitive-bandwidth” of non-majority students, which in turn, affects their academic performance [6, 7].

The issue of not accounting for arbitrary privileges can be broken down into two main problems: the Before and After problems. In the Before problem, arbitrary and morally irrelevant privileges weigh heavily on the outcomes of formally fair competitions as people with more privilege are often in a better position to build relevant qualifications. This can be seen in the problem described above of predicting students’ performance for admissions. The After problem is an effect of formally fair, but not arbitrary-privilege aware, competition in that the winner of a competition (e.g., getting hired or admitted to a top-tier college) is then in the position to gain even more success and qualifications. It introduces a compounding snow-ball effect in that winners win faster, but losers also lose faster [2]. Overall, formal EOP compounds both privilege and disprivilege, which is referred to as discrimination laundering [8].

Substantive (Rawls’) EOP

Substantive EOP addresses the discrimination laundering problem in that it requires all individuals to have the same opportunity to gain qualifications. It aims to give everyone a fair chance at success in a competition. For example, making all extra curricular activities and high-school opportunities equally available to all students regardless of wealth or social status. Substantive EOP is often equated with Rawls’ fair EOP which states that all individuals, regardless of how rich or poor they are born, should have the same opportunities to develop their talents in order to allow people with the same talents and motivation to have the same opportunities [9]. In fair machine learning, substantive EOP is often implemented through metrics such as statistical parity and equalized odds, which assume that talent and motivation are equally distributed among sub-populations.

But, the assumption that these talents are equally distributed often does not hold in practice. By the time a machine learning system is being used to make a decision, it is normally too late to provide individuals with the opportunity to develop qualifications. In this lens, fair machine learning has re-written Rawls’ EOP to say that a competition must only measure a candidate on the basis of their talent, while ignoring qualifications that reflect the candidates unequal developmental opportunities prior to the point of the competition [2].

Luck-Egalitarian EOP

Furthering the ideals of substantive EOP, luck-egalitarian EOP enforces that a person’s outcome should be affected only by their choices, not their circumstances [10]. For example, a student with rich parents who did not try hard in their studies should not have an advantage over a student with poor parents who did work hard in being admitted to a university. Overall, luck-egalitarian EOP is an attractive idea, and several metrics fall into this category (e.g., predictive parity, conditional use accuracy, test fairness, and well calibration), but the difficulty of separating choice from circumstance is non-trivial, and in practice, quite difficult to implement.

A few solutions for separation have been proposed. Economist and political scientist John Roemer proposed instead of trying to separate an individual’s qualifications into effects of consequence and choice, we should instead control for certain matters of consequence (such as, race, gender, and disability) that will impact a person’s access to opportunities to develop qualifications [11]. While this solution solves the separation problem, another issue of sub-group comparison emerges. We can compare apples to apples, and oranges to oranges, but we are now unable to compare apples to oranges [2]. Unfortunately, the EOP frameworks offer no solution to this problem of overall ranking.

Another problem in luck-egalitarian EOP is the separation of efforts in addition to circumstance [2]. It may be the case that a wealthy student works hard at their studies, i.e., the circumstance of being wealthy interacts with the effort of the student. This effect of entanglement is nearly impossible to separate. But, fortunately, this separation is only required when the circumstance gives access to a broad range of advantages. For instance, if a student’s family wealth status allows them to gain an advantage over all other students in almost every competition (not just university admission, but also job hiring or access to other opportunities), then there is a fairness problem. This is because there is an indication that the arbitrary privilege or circumstance, and not the relevant skill, is being used as the basis for decision. On the other hand, if the student only has the advantage in the admissions process, then it could be due to their effort rather than their circumstance, and we may or may not have a matter of unfairness where we need to separate effort from circumstance.

Causal

The first formal investigation into causality was done by the Greek philosopher Aristotle, who in 350 BC, published his two famous treatise, Physics and Metaphysics. In these treatise, Aristotle not only opposed the previously proposed notions of causality for not being grounded in any solid theory [12], but he also constructed a taxonomy of causation which he termed “the four causes.” In order to have proper knowledge, he deemed that we must have grasped its cause, and that giving a relevant cause is necessary and sufficient in offering a scientific explanation. His four causes can be seen as the four types of answers possible when asked a question of “why.”

The material cause: “that out of which” (something is made). E.g, the marble of a statue.
The formal cause: “the form”, “the account of what-it-is-to-be.” E.g, the shape of the statue.
The efficient cause: “the primary source of the change or rest.” E.g, the artist/sculptor of the marble statue.
The final cause: “the end, that for the sake of which a thing is done.” E.g, the creation of a work of art.

Despite giving four causes, Aristotle was not committed to the idea that every explanation had to have all four. Rather, he reasoned that any scientific explanation required up to four kinds of cause [12].

Another important philosopher who worked on causality was the 18th century Scottish philosopher David Hume. Hume rejected Aristotle’s taxonomy and instead insisted on a single definition of cause. This is despite the fact that he himself could not choose between two different, and later found to be incompatible, definitions [13]. In his Treatise of Human Nature, Hume states that “several occasions of everyday life, as well as the observations carried out for scientific purposes, in which we speak of a condition A as a cause and a condition B as its effect, bear no justification on the facts, but are simply based on our habit of observing B after having observed A” [14]. In other words, Hume believed that the cause-effect relationship was a sole product of our memory and experience [13]. Later, in 1739, Hume published An Enquiry Concerning Human Understanding in which he framed causation as a type of correlation: “we may define a cause to be an object followed by another, and where all the objects, similar to the first, are followed by objects similar to the second. Or in other words, where, if the first object had not been, the second never had existed.” While he tried to pass these two definitions off as one by using “in other words,” David Lewis pointed out that the second statement is contradictory to the first as it explicitly invokes the notion of a counterfactual which, cannot be observed, only imagined [13].

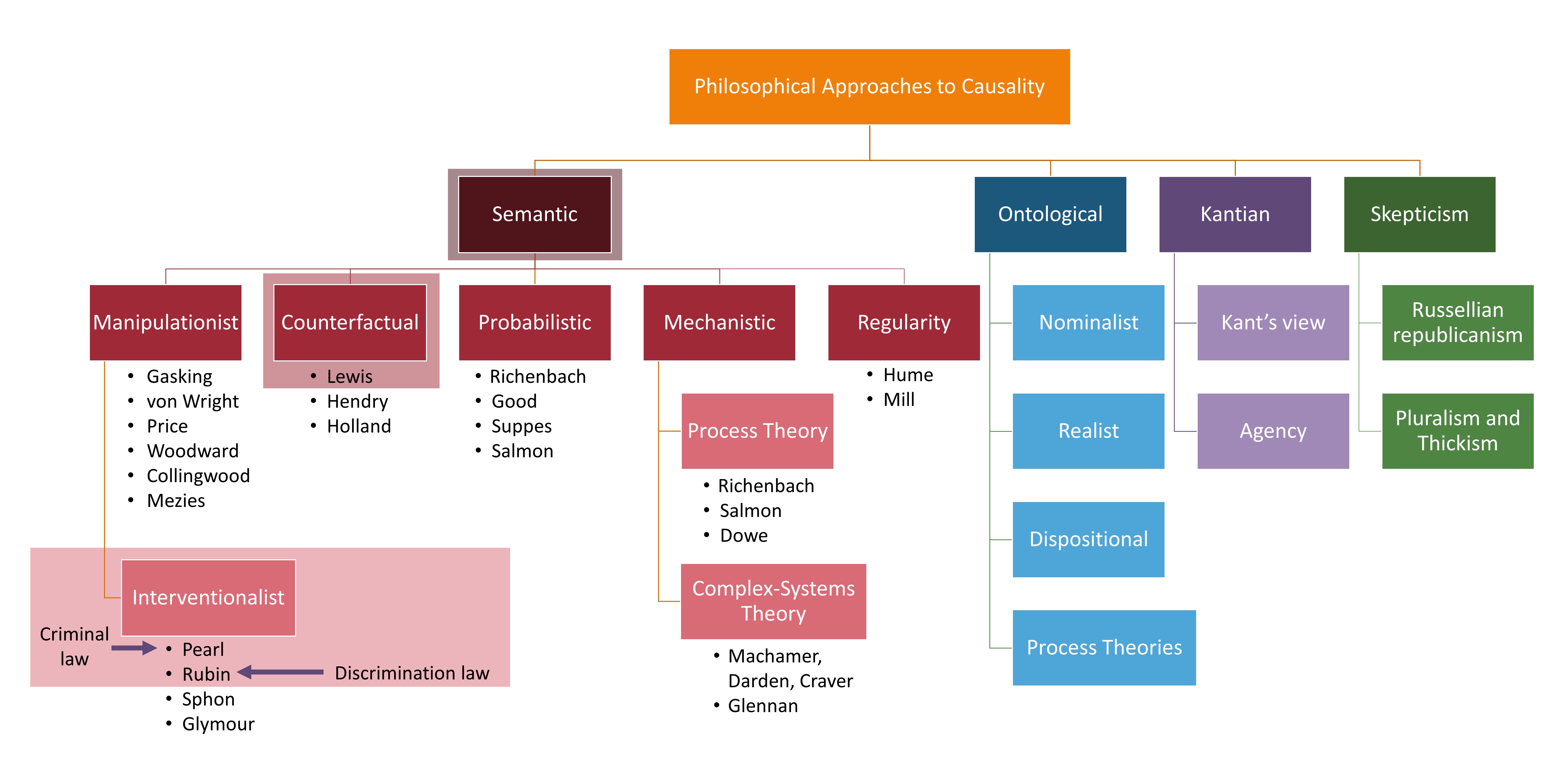
It is also important to note that Hume changed how philosophers approached causality by changing the question from “What is causality” to “What does our concept of causality mean?” In other words, he took a metaphysical question and turned it into an epistemological one [15]. This change allowed philosophers to take different approaches to answering the new question such as those based on semantic analyses, ontological stances, skepticism, and Kantian stances. Each of these approaches in turn garnered several theories of how to formulate an answer. A breakdown of all the approaches and theories can be seen in the figure above.

Regularity

The regularity theory implies that causes and effects do not usually happen just once, rather they happen as part of a regular sequence of events. For instance, today it rained causing the grass to be wet, but rain, no matter the day, produces this effect. This theory claims that in order to firmly say that one event causes another it must be that the cause is followed by the effect and that this cause-effect pair happens a lot. In other words, the cause and effect must be constantly conjoined [15]. Hume’s definition of causality from An Enquiry Concerning Human Understanding is a well regarded regularity theory.

Mechanistic

The mechanistic theory of causality says that explanations proceed in a downward direction: given an event to be explained, its mechanism (cause) is the structure of reality that is responsible for it [16]. I.e., two events are causally connected if and only if they are connected by an underlying physical mechanism. This is in contrast to causal explanations which often operate in a backwards direction: given an event to be explained, its causes are the events that helped produce it. There are two main kinds of mechanistic theory: 1) process theory which says that $A$ causes $B$ if and only if there is a physical process (something that transmits a mark or transmits a conserved physical quantity like energy-mass) that links $A$ and $B$; and complex-system theory which says that $A$ and $B$ are causally related if and only if they both occur in the same complex-system mechanism (a complex arrangement of events that are responsible for some final event or phenomenon because of how the events occur).

Probabilistic}

Probabilistic theories operate under the assumption that a cause occurring raises the probability of their corresponding effects. For example, “striking a match may not always be followed by its lighting, but certainly makes it more likely; whereas coincidental antecedents, such as my scratching my nose, do not” [15]](https://iep.utm.edu/causation/#H3). Probabilistic theories of causality are motivated by two main notions: 1) changing a cause makes a difference to its effects; and 2) this difference shows up in the probabilistic dependencies between the cause and effect [17]. Additionally, many probabilistic theorists go further and say that probabilistic dependencies provide necessary and sufficient conditions for causal connections. Further, many go one step farther and say that probabilistic dependencies give an analysis of a causal relation. I.e., that $C$ causes $E$ simply means that the corresponding probabilistic dependencies occur.

Counterfactual

David Lewis’s counterfactual theory of causation [18] starts with the observation that if a cause had not happened, the corresponding effect would not have happened either. A cause, according to Lewis in his 1973 article “Causation”, was “something that makes a difference, and the difference it makes must be a difference from what would have happened without it” [18]. He defined causal inference to be the process of comparing the world as it is with the closest counterfactual world. If $C$ occurs both in the actual and the closest counterfactual world without $A$, then it must be that A is not the cause of $C$. Many note that since he provided sparse practical guidance on how to construct counterfactual worlds, his theories when used alone have limited use to empirical research [18].

Additionally, it may seem odd that counterfactuals constitute a whole separate theory and is not combined with the manipulation or interventionalist theories. But this is because interventionalist theories shift the approach from pure conceptual analysis to something more closely related to causal reasoning and focused on investigating and understanding causation than producing a complete theory [15]. This point additionally highlights why interventionalist approaches to both causal frameworks and causality-based machine learning fairness metrics are popular. The PO and SCM frameworks of Rubin and Pearl have risen to the forefront since their treatment of causality is no longer purely theoretical. They give tools and methods to actually implement causality-based notions rather than just speak to “what does our concept of causality mean.” One might say that the probabilistic theories technically gave a mathematical framework for a possible implementation, but in reality, they did not produce any new computational tools or suggest methods for finding causal relationships and so were abandoned for using interventionalist approaches instead [19].

Manipulation and Interventionalist

Manipulability theories equate causality with manipulability. In these cases, $X$ causes $Y$ only when you can change $X$ in order to change $Y$. This idea makes intuitive sense with how we think about causation since we often ask causal questions in order to change some aspect of our world. For instance, asking what causes kids to drop out of school so that we might try to increase retention rates. But, most philosophical discussion on manipulability theories have been harsh. Two complaints have been that manipulability theories are circular in nature and that they produce theories that are not valid since it depends on being able to actually manipulate the variable at hand to cause an effect, i.e., changing the race of a person to observe if the final effect differed [20]. The interventionist framework was proposed to overcome these issues and to present a plausible version of a manipulability theory.

Interventionalist approaches attempt to perform a surgical change in $A$ which is of such a character that if any change occurs in $B$, it occurs only as a result of its causal connection to $A$. In other words, the change in $B$, that is produced by the surgical change of $A$ should be produced only via a causal path that goes through $A$ [20]. Both Judea Pearl and Donald Rubin have interventional theories - Rubin in the PO framework and Pearl in the SCM framework. Pearl noted that causal events can be formally represented in a graph which enabled the display of the counterfactual dependencies between the variables [13, 21]. The counterfactual dependencies are then analyzed against what would happen if there was an (hypothetical) intervention to alter the value of only a specified variable (or variables). Pearl suggested that formulating causal hypotheses in this manner offered the mathematical tools for analyzing empirical data [15].

In contrast with Pearl, Rubin advocated for the treatment of causation in terms of more manipulation-based ideas, meaning that causal claims involving causes that are un-manipulable in the principle are defective [20]. Un-manipulable does not mean variables that cannot be manipulated due to practical reasons, but rather variables that do not have a clear conception of what it would take to manipulate them, such as race, species, and gender.